Boxplots sind Diagramme, die Ihnen zeigen, wie die Werte Ihrer Daten verteilt sind. Hier erfahren Sie, wie Sie ein Boxplot lesen und sogar Ihr eigenes erstellen können.
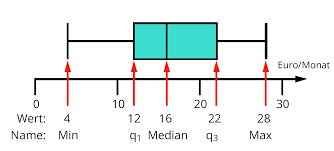
Ein Boxplot, auch als Boxplot, Boxplots oder Box-and-Whisker-Plot bekannt, ist eine standardisierte Methode zur Darstellung der Verteilung eines Datensatzes auf Grundlage seiner fünfstelligen Zusammenfassung der Datenpunkte: „Minimum“, erstes Quartil [Q1], Median, drittes Quartil [Q3] und „Maximum“. Hier ein Beispiel.
Boxplots geben Aufschluss über Ausreißer und ihre Werte. Sie geben außerdem Aufschluss darüber, ob Ihre Daten symmetrisch sind, wie eng Ihre Daten gruppiert sind und ob und wie Ihre Daten verzerrt sind .\
Wie immer ist der Code, der zur Erstellung der Grafiken verwendet wurde, auf meinem GitHub verfügbar . Damit können wir loslegen.
Was ist ein Boxplot?
Ein Boxplot ist ein Diagramm, das visuell darstellt, wie die 25., 50. und 75. Perzentilwerte sowie die Minimal-, Maximal- und Ausreißerwerte eines Datensatzes verteilt sind und wie sie im Vergleich zueinander aussehen.
Boxplots werden als Box mit einer vertikalen Linie in der Mitte und horizontalen Linien an beiden Seiten (sogenannte „Whisker“) dargestellt. Die Box wird verwendet, um den Interquartilsabstand (IQR) darzustellen – oder die 50 Prozent der Datenpunkte, die über dem ersten Quartil und unter dem dritten Quartil liegen – im gegebenen Datensatz. Die Whisker werden verwendet, um die Variabilität der minimalen, maximalen und eventuellen Ausreißerdatenpunkte im Vergleich zum IQR darzustellen (je länger der Whisker, desto größer die Variabilität der an den IQR angehängten Datenpunkte).
Die linke Seite der Box stellt das erste Quartil (Q1; das 25. Perzentil) der Daten dar, die Linie in der Mitte der Box stellt den Median (Q2; das 50. Perzentil) der Daten dar und die rechte Seite der Box stellt das dritte Quartil (Q3; das 75. Perzentil) der Daten dar. Wenn innerhalb der Box ein Punkt-, Kreuz- oder Rautensymbol vorhanden ist, stellt dies den Mittelwert der Daten dar.
Was die Whisker des Boxplots betrifft, zeigt der linke Whisker den minimalen Datenwert und seine Variabilität im Vergleich zum IQR. Der rechte Whisker zeigt den maximalen Datenwert und seine Variabilität im Vergleich zum IQR. Whisker helfen auch dabei, Ausreißerwerte im Vergleich zu den übrigen Daten darzustellen, da Ausreißer außerhalb der Whisker-Linien liegen.
- Median (Q2/50. Perzentil) : Der mittlere Wert des Datensatzes
- Erstes Quartil (Q1/25. Perzentil) : Die mittlere Zahl zwischen der kleinsten Zahl (nicht dem „Minimum“) und dem Median des Datensatzes
- Drittes Quartil (Q3/75. Perzentil) : Der mittlere Wert zwischen dem Median und dem höchsten Wert (nicht dem „Maximum“) des Datensatzes
- Interquartilsabstand ( IQR ) : 25. bis 75. Perzentil
- Schnurrhaare (blau dargestellt)
- Ausreißer (als grüne Kreise dargestellt)
- “Minimum” :Q1 – 1.5*IQR
- „Maximum“ :Q3 + 1.5*IQR
Wann wird ein Boxplot verwendet?
Ein Boxplot kann hilfreich sein, wenn Sie aus einem Datensatz/einer Verteilung mehr Informationen benötigen als nur die Maße der zentralen Tendenz (Mittelwert, Median und Modus). Boxplots können die Variabilität oder Streuung aller in einem Datensatz vorhandenen Datenpunkte veranschaulichen und einen guten Hinweis auf Ausreißer und die Symmetrie der Daten geben.
Obwohl Boxplots im Vergleich zu einem Histogramm oder Dichtediagramm primitiv erscheinen mögen, haben sie den Vorteil, dass sie weniger Platz beanspruchen, was beim Vergleich von Verteilungen zwischen vielen Gruppen oder Datensätzen nützlich ist.
Was einen Ausreißer, ein „Minimum“ oder ein „Maximum“ definiert, ist möglicherweise noch nicht klar. Der nächste Abschnitt versucht, dies für Sie zu klären.
Boxplot auf einer Normalverteilung
Das obige Bild ist ein Vergleich eines Box-and-Whisker-Plots einer nahezu normalen Verteilung und der Wahrscheinlichkeitsdichtefunktion (PDF) für eine normale Verteilung. Der Grund, warum ich Ihnen dieses Bild zeige, ist, dass es alltäglicher ist, sich eine statistische Verteilung anzusehen, als sich ein Boxplot anzusehen. Mit anderen Worten, es könnte Ihnen helfen, ein Boxplot zu verstehen.
In diesem Abschnitt werden folgende Themen behandelt:
- Ausreißer sind (bei einer Normalverteilung) 0,7 Prozent der Daten.
- Was ein „Minimum“ und ein „Maximum“ sind.
Wahrscheinlichkeitsdichtefunktion
Dieser Teil des Beitrags ist meinem Artikel zur 68–95–99,7-Regel (Normalverteilung) sehr ähnlich, wurde jedoch für ein Boxplot angepasst. Um zu verstehen, woher die Prozentsätze kommen, ist es wichtig, die Wahrscheinlichkeitsdichtefunktion (PDF) zu kennen. Eine PDF wird verwendet, um die Wahrscheinlichkeit anzugeben, dass die Zufallsvariable in einen bestimmten Wertebereich fällt , anstatt einen bestimmten Wert anzunehmen. Diese Wahrscheinlichkeit ergibt sich aus dem Integral der PDF dieser Variable über diesen Bereich – das heißt, sie ergibt sich aus der Fläche unter der Dichtefunktion, aber über der horizontalen Achse und zwischen dem niedrigsten und dem höchsten Wert des Bereichs. Diese Definition ist möglicherweise nicht sehr sinnvoll, also klären wir sie auf, indem wir die Wahrscheinlichkeitsdichtefunktion für eine Normalverteilung grafisch darstellen. Die folgende Gleichung ist die Wahrscheinlichkeitsdichtefunktion für eine Normalverteilung:
Vereinfachen wir es, indem wir annehmen, wir haben einen Mittelwert ( μ) von 0und eine Standardabweichung ( σ) von 1.
Sie können dies mit beliebigen Mitteln grafisch darstellen, ich habe mich jedoch für die Verwendung von Python entschieden .
Die obige Grafik zeigt nicht die Wahrscheinlichkeit von Ereignissen, sondern deren Wahrscheinlichkeitsdichte. Um die Wahrscheinlichkeit eines Ereignisses innerhalb eines bestimmten Bereichs zu erhalten, müssen wir integrieren. Angenommen, wir möchten die Wahrscheinlichkeit ermitteln, dass ein zufälliger Datenpunkt innerhalb der Interquartilsabstand-Standardabweichung des Mittelwerts liegt. Dann müssen wir von bis .6745integrieren . Dies können Sie mit SciPy tun.-.6745.6745
Dasselbe können Sie für „Minimum“ und „Maximum“ tun.
Wie bereits erwähnt, handelt es sich bei den restlichen 0,7 Prozent der Daten um Ausreißer.
Es ist wichtig zu beachten, dass für jede PDF der Bereich unter der Kurve eins sein muss (die Wahrscheinlichkeit, eine beliebige Zahl aus dem Funktionsbereich zu ziehen, ist immer eins).
So erstellen und interpretieren Sie ein Boxplot
Dieser Abschnitt basiert größtenteils auf einem kostenlosen Vorschauvideo aus meinem Kurs „Python für Datenvisualisierung“ . Im letzten Abschnitt haben wir ein Boxplot auf einer Normalverteilung durchgegangen, aber da Sie natürlich nicht immer eine zugrunde liegende Normalverteilung haben, gehen wir nun durch, wie Sie ein Boxplot auf einem realen Datensatz verwenden. Dazu verwenden wir den Datensatz „Breast Cancer Wisconsin (Diagnostic)“ . Wenn Sie kein Kaggle- Konto haben , können Sie den Datensatz von meinem GitHub herunterladen .
Daten einlesen
Der folgende Code liest die Daten in einen Pandas- DataFrame.
So erstellen Sie ein Boxplot
Wir verwenden unten ein Boxplot, um die Beziehung zwischen einem kategorischen Merkmal (bösartiger oder gutartiger Tumor) und einem kontinuierlichen Merkmal ( area_mean) zu analysieren.
Es gibt mehrere Möglichkeiten, ein Boxplot mit Python zu zeichnen. Sie können ein Boxplot mit Seaborn, Matplotlib oder Pandas zeichnen.
Seeborn
Der folgende Code übergibt den Pandas-DataFrame dfan Seaborns boxplot.
Matplotlib
Ich habe die Boxplots, die Sie in diesem Beitrag sehen, mit Matplotlib erstellt. Dieser Ansatz kann weitaus mühsamer sein, bietet Ihnen aber ein höheres Maß an Kontrolle.
Pandas
Sie können ein Boxplot erstellen, indem Sie es .boxplot()in Ihrem DataFrame aufrufen. Der folgende Code erstellt ein Boxplot der area_meanSpalte in Bezug auf verschiedene Diagnosen.
Gekerbtes Boxplot
Mit dem gekerbten Boxplot können Sie Konfidenzintervalle (standardmäßig 95-Prozent- Konfidenzintervall ) für die Mediane jedes Boxplots auswerten.
So interpretieren Sie ein Boxplot
In der Datenwissenschaft geht es um die Kommunikation von Ergebnissen. Denken Sie also daran, dass Sie Ihre Boxplots mit ein wenig Arbeit immer noch etwas schöner gestalten können (den Code finden Sie hier ).
Mithilfe der Grafik können wir die Spannweite und Verteilung der area_meanbösartigen und gutartigen Diagnosen vergleichen. Wir stellen fest, dass es eine größere Variabilität für den Bereichsmittelwert bösartiger Tumore sowie größere Ausreißer gibt.
Da sich die Kerben in den Boxplots nicht überschneiden, können Sie mit 95-prozentiger Sicherheit davon ausgehen, dass die wahren Mediane voneinander abweichen.
Hier sind noch ein paar weitere Dinge, die Sie bei Boxplots beachten sollten:
- Sie können die Daten jederzeit aus dem Boxplot extrahieren, falls Sie die numerischen Werte für die verschiedenen Teile eines Boxplots wissen möchten.
- Matplotlib schätzt nicht zuerst eine Normalverteilung, sondern berechnet die Quartile aus den geschätzten Verteilungsparametern. Der Median und die Quartile werden direkt aus den Daten berechnet. Mit anderen Worten: Ihr Boxplot kann je nach Verteilung Ihrer Daten und Größe der Stichprobe anders aussehen (z. B. asymmetrisch und mit mehr oder weniger Ausreißern ).
Hoffentlich waren das nicht zu viele Informationen zu Boxplots. In meinem nächsten Tutorial geht es um die Verwendung und Erstellung einer Z-Tabelle (Standardnormaltabelle) . Wenn Sie Fragen oder Anmerkungen zum Tutorial haben, können Sie uns gerne über YouTube oder Twitter erreichen .