Erläuterung der zeitlichen Komplexität und des Algorithmus von Bubble Sort

Bubble sort ist ein Sortieralgorithmus, der Vergleichsmethoden zum Sortieren eines Arrays verwendet. Die durchschnittliche Zeitkomplexität beträgt O(n^2). Hier erfahren Sie, was Sie wissen müssen.

Bubble sort ist ein Sortieralgorithmus , der mit dem ersten Element eines Arrays beginnt und es mit dem zweiten Element vergleicht. Wenn das erste Element größer als das zweite ist, werden sie vertauscht. Dieser Vorgang wird bis zum Ende des Arrays fortgesetzt, wobei die größten Elemente nach oben „sprudeln“. Die Zeitkomplexität im schlimmsten Fall beträgt O(n²) und die Zeitkomplexität im besten Fall O(n).

Als Softwareentwickler und Datenwissenschaftler halten wir Sortierfunktionen wie diese oft für selbstverständlich. Diese Algorithmen sind vielleicht nicht die glamourösesten oder am meisten diskutierten Aspekte unserer Arbeit, aber sie spielen eine entscheidende Rolle in den Technologien, die wir täglich nutzen. Stellen Sie sich beispielsweise vor, Sie versuchen, die Kontaktliste auf Ihrem Telefon zu organisieren, ohne eine Möglichkeit zum alphabetischen Sortieren zu haben, oder Produkte auf einer E-Commerce- Website nach Preis und Kategorie zu sortieren. 

Obwohl die meisten Programmiersprachen wie Java , Python , C# usw. über integrierte Funktionen für gängige Sortieralgorithmen verfügen, ist es dennoch wichtig zu verstehen, wie diese Algorithmen funktionieren. Auf diese Weise können wir fundierte Entscheidungen darüber treffen, welchen Algorithmus wir auf der Grundlage seiner räumlichen und zeitlichen Komplexität verwenden, insbesondere wenn wir als Datenwissenschaftler mit großen Datensätzen arbeiten. Unterschätzen Sie also nicht die bescheidene Sortierfunktion. Sie ist vielleicht nicht der Star der Show, aber sie ist der heimliche Held der Technologiebranche.

In diesem Artikel werden wir uns mit dem Bubble sort-Algorithmus befassen und seine Implementierung in Python und JavaScript untersuchen . Wir werden uns auch die Intuition hinter dem Algorithmus genauer ansehen und Überlegungen zur zeitlichen und räumlichen Komplexität diskutieren. Am Ende haben Sie ein solides Verständnis dafür, wann es angemessen ist, den Bubble sort-Algorithmus in Ihren Programmen zu verwenden, sowie einen Überblick über seine räumlichen und zeitlichen Komplexitäten.

Was ist Bubble sort?

Wenn man versucht, einen Algorithmus zu verstehen, ist es immer hilfreicher, sich zunächst das Konzept anzueignen und sich erst später daran zu erinnern. Bubble sort ist hier keine Ausnahme.

Um ein Array [2, 3, 4, 5, 1]mit dem Bubble sort-Algorithmus aufsteigend zu sortieren, beginnen wir mit dem ersten Element [2]und vergleichen es mit dem zweiten Element [3]. Wenn das erste Element größer als das zweite ist, vertauschen wir sie. Wir setzen diesen Prozess des Vergleichens von Elementpaaren fort, bis wir das Ende des Arrays erreichen. Auf diese Weise werden die größten Elemente an das Ende des Arrays verschoben und die kleinsten Elemente an den Anfang des Arrays.

Der Name „Bubble sort“ bezieht sich auf die Art und Weise, wie größere Elemente an den Anfang oder das Ende des Arrays „sprudeln“, während sie wiederholt mit kleineren Elementen verglichen und ausgetauscht werden. Am Ende des Sortiervorgangs ist das Array vollständig in aufsteigender Reihenfolge sortiert.

Zeitliche und räumliche Komplexität des Bubble sort

Datenwissenschaftler müssen die Leistung eines Sortieralgorithmus und seinen Zeit-/Platzbedarf verstehen . So können Sie je nach Ihrer spezifischen Situation den besten Sortieralgorithmus auswählen, da viele Optionen verfügbar sind.

Wenn Bubble sort auf ein Array angewendet wird , das bereits in aufsteigender Reihenfolge vorliegt, ist nur ein Durchlauf durch das gesamte Array erforderlich. Dies gilt als Best-Case-Szenario. In der Praxis kommt dies jedoch nur manchmal vor, und Bubble sort erfordert normalerweise n(n-1)/2 Vertauschungen oder Vergleiche, um ein sortiertes Array zu erhalten.

Die durchschnittliche/schlechteste Zeitkomplexität des Bubble sort-Algorithmus beträgt O(n²), da wir das Array so oft durchlaufen müssen, wie Paare in einem bereitgestellten Array vorhanden sind. Wenn Zeit ein Faktor ist, kann es daher bessere Optionen geben.

• Zeitliche Komplexität im schlimmsten Fall: O(n²).
• Durchschnittliche Zeitkomplexität: O(n²).
• Best-Case-Zeitkomplexität: O(n), das Array ist bereits sortiert.

Was die Speicherkomplexität betrifft, so benötigen wir keinen zusätzlichen Speicherplatz, um den Algorithmus auszuführen, da wir nur die Elemente untereinander ausgetauscht und nie etwas gespeichert haben. Das ist erstaunlich, denn es bedeutet, dass die Speicherkomplexität konstant oder O(1) ist. Dies macht es zu einem In-Place-Algorithmus, der funktioniert, indem er die Eingabe direkt ändert.

So funktioniert der Bubble sort-Algorithmus

Schauen wir uns den Bubble sort-Algorithmus in Aktion an. Nachfolgend finden Sie eine Liste ungeordneter Zahlen, die wir mithilfe von Bubble sort organisieren werden:

Der erste Schritt besteht darin, sich nur auf die ersten beiden Zahlen zu konzentrieren, die in diesem Beispiel 5und sind 9. Sie können es sich wie im Bild unten gezeigt vorstellen, indem Sie nur die beiden Elemente 5und berücksichtigen:9

Dann müssen Sie feststellen, ob die Zahlen in der Blase in der richtigen Reihenfolge sind. Wenn sie nicht in der richtigen Reihenfolge sind, vertauschen Sie sie, um sie richtig zu machen. Zum Glück für uns sind sie bereits in aufsteigender Reihenfolge angeordnet. 5ist kleiner als 9, also kommt es vor 9. Das bedeutet, dass wir nichts weiter tun müssen. Wir verschieben unsere Blase einen Schritt weiter, und zwar so:

Wir führen den gleichen Schritt in der nächsten Iteration des Arrays durch. Dieses Mal 9ist jedoch größer als 1, aber es liegt auch davor. Um das zu korrigieren, wird die Position beider Elemente vertauscht. So sieht die Liste jetzt aus:

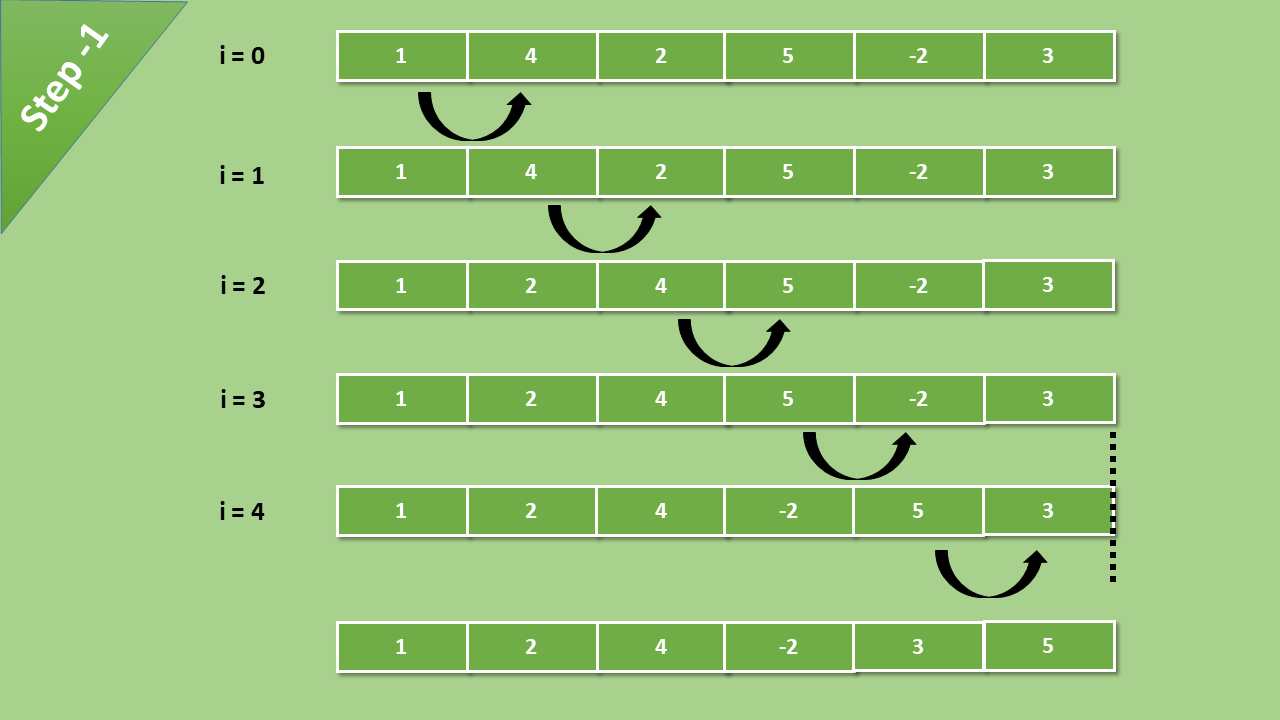
Nachdem die Elemente nun vertauscht sind, schreitet die Blase zu den nächsten Paaren fort. Und die Schritte werden wiederholt, bis die letzten Paare im Array einer Prüfung auf Vertauschung unterzogen wurden. Der erste Durchlauf durch das Array sieht folgendermaßen aus:

Der Bubble sort-Algorithmus ist eine einfache, aber effektive Methode zum Sortieren eines Arrays von Elementen. Dabei wird das Array wiederholt durchlaufen und Elementpaare verglichen. Wenn sie nicht in der richtigen Reihenfolge sind, werden ihre Positionen vertauscht. Dieser Vorgang wird wiederholt, bis das gesamte Array sortiert ist.

Zu beachten ist, dass die Anzahl der zum Sortieren eines Arrays erforderlichen Durchläufe der Anzahl der Elemente im Array entspricht. Beispielsweise muss ein Array mit sechs Elementen sechs Durchläufe durchlaufen, um vollständig in aufsteigender Reihenfolge sortiert zu werden.

Es ist jedoch möglich, den Bubble sort-Algorithmus effizienter zu gestalten, indem man die Anzahl der Operationen oder Durchläufe begrenzt, die am Array durchgeführt werden. Dies liegt daran, dass das letzte Element des Arrays immer den Maximalwert hat, sodass es bei zukünftigen Durchläufen des Arrays nicht notwendig ist, alle Elemente über diesen Punkt hinaus weiter zu vergleichen. Wir werden diese Optimierung in Aktion sehen, wenn wir in den folgenden Abschnitten den Bubble sort-Algorithmus in Python und JavaScript implementieren.

So implementieren Sie Bubble sort in Python

In diesem Abschnitt wird der Bubble sort-Algorithmus mit Python implementiert. Wir werden uns eine naive Implementierung und eine effizientere Version des Bubble sort-Algorithmus ansehen.

Initialisieren Sie ein Python-Array mit ganzzahligen Elementen:

Definieren Sie eine Funktion mit dem Namen bubble Sort , die in ihrem Parameter mit dem Namen ein Array akzeptiert data. Versuchen wir zunächst, das Array zu durchlaufen, das alle Elemente austauscht, die die Bedingung erfüllen, dass wir einen Austauschvorgang zwischen diesen beiden Elementen ausführen, wenn das linke Element an einem bestimmten Index größer als ein Element rechts ist.

Zu beachten ist die Zuweisung des linken Elements in jeder Iteration zu einer temporären Variable tempValue und die anschließende Zuweisung des rechten Elements zur temporären Variable.

Wenn der obige Codeausschnitt mit einem unsortierten Array als Argument aufgerufen wird, führt er die bubble Sort Funktion pass einmal auf dem Array aus. Und in den meisten Fällen wird das Array nicht vollständig in aufsteigender Reihenfolge sortiert.

Um dies zu beheben, müssen wir das Array, das wir sortieren möchten, so oft durchlaufen, wie es Paarkombinationen gibt. Die Anzahl der durchzuführenden Iterationen ist die Länge des unsortierten Arrays im Quadrat (len(unsortedArrray)²). Dies ist die naive Implementierung.

Wenn Sie die Bubble sort-Funktion erneut mit dem unsortierten Array als Argument ausführen, erhalten Sie ein aufsteigend sortiertes Array als Ausgabe.

Bubble-Sort-Algorithmus optimiert

Obwohl die naive Version des Bubble sort-Algorithmus funktioniert, weist sie einige unnötige und redundante Operationen auf. Insbesondere vergleicht sie Elemente am Ende des Arrays, die bereits die im Array vorhandenen Maximalwerte aufweisen. Dies liegt daran, dass der Bubble sort-Algorithmus bei jedem Durchlauf durch das Array die maximalen Elementwerte an das Ende des Arrays verschiebt.

Um den Bubble sort-Algorithmus zu optimieren, können wir die Anzahl der erforderlichen Swap-Operationen reduzieren, indem wir den Teil des Arrays im Auge behalten, den wir für den Vergleich berücksichtigen möchten. Wir können dies tun, indem wir mit der maximalen Länge des Arrays beginnen und diese nach jedem Durchgang um eins verringern, wodurch der Bereich des Arrays reduziert wird, auf den die Swap-Operation einwirkt. Auf diese Weise können wir bei jedem Durchgang Vergleiche mit den letzten Elementen des Arrays vermeiden, die sich bereits an der richtigen Position befinden.

Durch diese Optimierung können wir den Bubble sort-Algorithmus effizienter machen und die Anzahl unnötiger Operationen reduzieren, die er ausführt.

Um sicherzustellen, dass der obige Code lesbar und effizient ist, könnten weitere Refactorings durchgeführt werden. 

Unten finden Sie eine Implementierung desselben Algorithmus in JavaScript, einer bei Datenpraktikern und Softwareentwicklern beliebten Programmiersprache.

So implementieren Sie den Bubble sort-Algorithmus in JavaScript

Vorteile des Bubble sort-Algorithmus

Der Bubble sort-Algorithmus ist vielleicht nicht der bekannteste oder am meisten geschätzte Sortieralgorithmus, aber er ist auch keine schlechte Option. Mit einer Zeitkomplexität von O(n²) und einer Raumkomplexität von O(1) ist er ein einfacher Algorithmus, der für Anfänger leicht zu verstehen ist. Seine geringe Geschwindigkeit kann ihn jedoch für bestimmte Anwendungen weniger praktisch machen.

Trotz seiner Einschränkungen kann der Bubble sort-Algorithmus ein nützlicher Ausgangspunkt zum Erlernen von Sortieralgorithmen und Datenstrukturen sein. Er ist eine gute Möglichkeit, ein grundlegendes Verständnis der Funktionsweise dieser Algorithmen zu erlangen und kann Ihnen helfen, eine Grundlage für das spätere Erlernen komplexerer Algorithmen zu schaffen superconductor.

Allerdings ist der Bubble sorts-Algorithmus möglicherweise nicht die beste Wahl für zeitkritisches Material, da seine langsame Geschwindigkeit unerschwinglich sein kann. Wenn Sie jedoch bereit sind, etwas Platz für Zeit zu opfern, kann er für Sie gut funktionieren. Letztendlich hängt die Wahl des Sortieralgorithmus von Ihren spezifischen Anforderungen und Zielen ab. Indem Sie sich über den Bubble sorts-Algorithmus informieren, können Sie fundiertere Entscheidungen darüber treffen, welcher Algorithmus für Ihre Anforderungen am besten geeignet ist.

Häufig gestellte Fragen